Obraz krychle
Úloha číslo: 4422
Lineární zobrazení \(f:\mathbb R^3\to\mathbb R^3\) transformuje krychli \(ABCDEFGH\) na rovnoběžnostěn t.ž. \(f(A)=\mathbf 0\), \(f(B)=(4,-3{,}2)^T\), \(f(D)=(-8{,}3,7)^T\) a \(f(E)=(5,-2,-2)^T\).
Určete obrazy zbývajících čtyř vrcholů krychle.
Řešení
Pro jednoduchost předpokládejme, že jde o jednotkovou krychli s vrcholem \(A\) v počátku a jejíž vrcholy \(B, D\) a \(E\) tvoří kanonickou bázi.
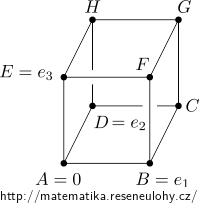
Využijeme linearitu \(f\), čili:
\(f(C)=f(B+D)=f(B)+f(D)=(4,-3{,}2)^T+(-8{,}3,7)^T=(-4{,}0,9)^T\), \(f(F)=f(B+E)=f(B)+f(E)=(4,-3{,}2)^T+(5,-2,-2)^T=(9,-5{,}0)^T\), \(f(G)=f(B+D+E)=f(B)+f(D)+f(E)=(4,-3{,}2)^T+(-8{,}3,7)^T+(5,-2,-2)^T=(1,-2{,}7)^T\), \(f(H)=f(D+E)=f(D)+f(E)=(-8{,}3,7)^T+(5,-2,-2)^T=(-3{,}1,5)^T\).V skutečnosti postačí vzít jakoukoli krychli s \(A\) v počátku, protože jsme nijak nevyužili konkrétní souřadnice bodů \(B, D\) a \(E\). Pro \(A\ne\mathbf 0\) by zobrazení \(f\) nebylo lineární. V tomto případě by šlo o afinní bijekci, protože obrazy tří lineárně nezávislých vektorů by byly lineárně nezávislé, ale vzor počátku by nebyl počátek.
Odpověď
Obrazy zbývajících vrcholů jsou \(f(C)=(-4{,}0,9)^T\), \(f(F)=(9,-5{,}0)^T\), \(f(G)=(1,-2{,}7)^T\) a \(f(H)=(-3{,}1,5)^T\).Komentář
Pokud by však obrazy bodů \(B,D\) a \(E\) byly lineárně závislé, nemusí už být vzorem nulového vektoru nulový vektor, čili \(A=\boldsymbol 0\)
Ovšem v těchto případech dostaneme stejné řešení. Jelikož jde o krychli, dávají rozdíly \(B-A\) a \(C-D\) stejný vektor. Odtud \(f(B-A)=f(C-D) \Rightarrow f(B)-f(A)=f(C)-f(D) \Rightarrow f(C)=f(B)+f(D)-f(A)=f(B)+f(D)\).
Podobně pro další vrcholy.



