Pomocná úloha
Úloha číslo: 3260
Vyřešte následující problém LP simplexovou metodou. Na závěr znázorněte řešení graficky.
Varianta 1
\[\begin{eqnarray*} \max (3x_1+x_2) \\ x_1 - x_2 & \le & -1 \\ - x_1 - x_2 & \le & -3 \\ 2x_1 - x_2 & \le & 2 \\ x_1,x_2 & \ge & 0 \end{eqnarray*}\]
Řešení
Nejprve vyřešíme pomocnou úlohu s tabulkou:
\[\begin{eqnarray*} \max (-x_0) \\ - x_0 + x_1 - x_2 & \le & -1 \\ - x_0 - x_1 - x_2 & \le & -3 \\ - x_0 + 2x_1 - x_2 & \le & 2 \\ x_0,x_1,x_2 & \ge & 0 \end{eqnarray*}\] \[ \begin{array}{r|rrrrrr|r} 3 & -1 & 1 & -1 & 1 & 0 & 0 & -1 \\ 4^* & -1 & -1 & -1 & 0 & 1 & 0 & -3 \\ 5 & -1 & 2 & -1 & 0 & 0 & 1 & 2 \\ \hline & -1^* & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \]
Tabulku převedeme do konzistentního tvaru a pokračujeme simplexovou metodou.
\[ \begin{array}{r|rrrrrr|r} 3 & 0 & 2 & 0 & 1 & -1 & 0 & 2 \\ 0^* & 1 & 1 & 1 & 0 & -1 & 0 & 3 \\ 5 & 0 & 3 & 0 & 0 & -1 & 1 & 5 \\ \hline & 0 & 1 & 1^* & 0 & -1 & 0 & 3 \\ \end{array} \] \[ \begin{array}{r|rrrrrr|r} 3 & 0 & 2 & 0 & 1 & -1 & 0 & 2 \\ 2 & 1 & 1 & 1 & 0 & -1 & 0 & 3 \\ 5 & 0 & 3 & 0 & 0 & -1 & 1 & 5 \\ \hline & -1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \]
Získali jsme optimální řešení pomocné úlohy \((x_0,…,x_5)=(0{,}0,3{,}2,0{,}5)\), které je zároveň přípustným řešením původní úlohy (zapomeneme=li na \(x_0\)). Změníme tedy jenom účelovou funkci, vyjádříme ji vzhledem k nebázickým proměnným a řešíme dále:
\[ \begin{array}{r|rrrrrr|r} 3 & . & 2 & 0 & 1 & -1 & 0 & 2 \\ 2 & . & 1 & 1 & 0 & -1 & 0 & 3 \\ 5 & . & 3 & 0 & 0 & -1 & 1 & 5 \\ \hline & . & 3 & 1 & 0 & 0 & 0 & 0 \\ \end{array} \] \[ \begin{array}{r|rrrrrr|r} 3 & . & 2 & 0 & 1 & -1 & 0 & 2 \\ 2 & . & 1 & 1 & 0 & -1 & 0 & 3 \\ 5 & . & 3 & 0 & 0 & -1 & 1 & 5 \\ \hline & . & 2 & 0 & 0 & 1^* & 0 & -3 \\ \end{array} \]
Při volbě \(s=4\) ale vidíme, že hodnota účelové funkce je neomezená, čili úloha nemá žádné optimální řešení, což je vidět i z obrázku.
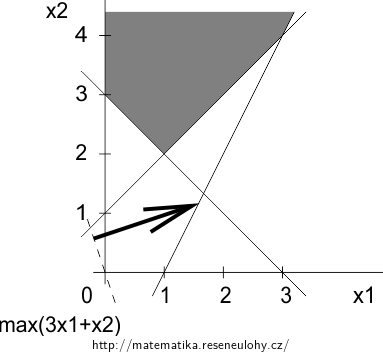
Varianta 2
\[\begin{eqnarray*} \max (3x_1+x_2) \\ x_1 - x_2 & \le & -1 \\ - x_1 - x_2 & \le & -3 \\ 2x_1 + x_2 & \le & 2 \\ x_1,x_2 & \ge & 0 \end{eqnarray*}\]
Řešení
Příklad řešíme obdobně, nejprve sestavíme tabulku, kterou hned upravíme na vhodný tvar:
\[ \begin{array}{r|rrrrrr|r} 3 & -1 & 1 & -1 & 1 & 0 & 0 & -1 \\ 4^* & -1 & -1 & -1 & 0 & 1 & 0 & -3 \\ 5 & -1 & 2 & -1 & 0 & 0 & 1 & 2 \\ \hline & -1^* & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \] \[ \begin{array}{r|rrrrrr|r} 3 & 0 & 2 & 0 & 1 & -1 & 0 & 2 \\ 0 & 1 & 1 & 1 & 0 & -1 & 0 & 3 \\ 5^* & 0 & 3 & 2 & 0 & -1 & 1 & 5 \\ \hline & 0 & 1 & 1^* & 0 & -1 & 0 & 3 \\ \end{array} \]
V další iteraci simplexové metody získáme tabulku \[ \begin{array}{r|rrrrrr|r} 3 & 0 & 2 & 0 & 1 & -1 & 0 & 2 \\ 0 & 1 & -1/2 & 0 & 0 & -1/2 & -1/2 & 1/2 \\ 2 & 0 & 3/2 & 1 & 0 & -1/2 & 1/2 & 5/2 \\ \hline & 0 & -1/2 & 0 & 0 & -1/2 & -1/2 & 1/2 \\ \end{array} \] s optimálním řešením pomocné úlohy \((x_0,…,x_5)=(1/2{,}0,5/2{,}2,0{,}0)\), což ovšem znamená, že původní úloha nemá žádné přípustné řešení. Obrázek naše řešení potvrdí.



