Platónská tělesa
Úloha číslo: 2678
Určete jaký úhel svírá tělesová úhlopříčka krychle s podstavou. Podobně spočítejte velikost úhlu mezi podstavou čyřstěnu a jednou z hran vedoucích do zbývajícího vrcholu. Spočítejte také velikost úhlu mezi úhlopříčkou osmistěnu a jeho libovolnou stěnou.
Jak spolu velikosti těchto úhlů souvisí?
Jaký je objem jednotkového čtyřstěnu a jednotkového osmistěnu?
Řešení
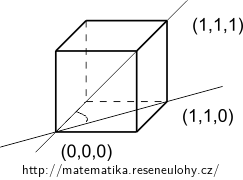
Krychle: úhel mezi úhlopříčkou \(\mathbf x^T=(1, 1, 1)\), a jejím průmětem do podstavy \(\mathbf y^T=(1, 1, 0)\) je \(\cos\alpha_1=\frac{\sqrt{6}}{3}\), \(\alpha_1\doteq 35^\circ\).
Čtyřstěn: Položíme-li vrcholy na body o souřadnicích \((0, 0, 0)\), \((0, 1, 1)\), \((1, 0, 1)\) a \(\mathbf x^T=(1, 1, 0)\), vyjde nám pro průmět \(\mathbf y^T=(\frac{1}{2}, \frac{1}{2}, 1)\), \(\cos\alpha_2=\frac{\sqrt{3}}{3}\), \(\alpha_2\doteq 55^\circ\). Pomocí vzorečku \(\cos{\alpha}=\sin(\frac{\pi}2-\alpha)\) snadno odvodíme, že \(\alpha_1+\alpha_2=\frac{\pi}2\).

Osmistěn: Vrcholy umístíme na \(A=(0, 0, 0)\), \(B=(1, 0, 1)\), \(C=(0, 1, 1)\), \((-1, 0, 1)\), \((0, -1, 1)\) a \(\mathbf x^T=(0, 0, 2)\). Potom průmět \(\mathbf x\) do stěny určené \(ABC\) je násobek vektoru \(\mathbf y^T=(\frac{1}{2}, \frac{1}{2}, 1)\) a odtud \(\cos\alpha_3=\frac{\sqrt{6}}{3}\), \(\alpha_3\doteq 35^\circ\) – tentýž úhel jsme spočítali u krychle.

Výška jednotkového čtyřstěnu je rovna sinu spočteného úhlu, t.j. \(\frac{\sqrt{6}}{3}\). Sama základna má výšku \(\frac{\sqrt{3}}{2}\), a odtud \(V=\frac{\sqrt{2}}{12}\)
Jednotkový osmistěn se skládá z dvou čtyřbokých jehlanů s jednotkovým čtvercem v podstavě a výškou \(d\), jejíž délka je rovna polovině délky úhlopříčky osmistěnu. Odtud \(V=\frac{2}{3}d\). Zbývá tedy spočítat délku úhlopříčky, ta je ale rovna úhlopříčce jednotkového čtverce, tedy \(V=\frac{\sqrt{2}}{3}\).



