Problém betonu
Úloha číslo: 3251
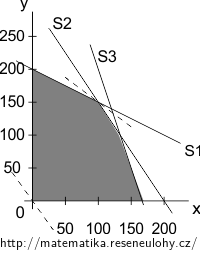
Betonárka vyrábí dva druhy betonových směsí B1 a B2. Na výrobu každé směsi jsou potřeba tři základní suroviny S1, S2 a S3, kterých je k dispozici omezené množství a to 80, 30 a 50 t/den. Dalí suroviny a zdroje jsou k dispozici v neomezeném množství. Na jeden kubík směsi B1 se spotřebuje 0.2t suroviny S1, 0.15t S2 a 0.3t S3. Podobně na kubík směsi B2 je třeba 0.4t S1, 0.1t S2 a 0.1t S3.
Varianta 1
Zformulujte úlohu lineárního programování pro maximalizaci zisku, kde odbytové ceny po odečtení nákladů jsou 300 eularů za kubík směsi B1 a 400 ER za kubík směsi B2. Graficky znázorněte prostor přípustných řešení a určete optimální řešení.
Varianta 2
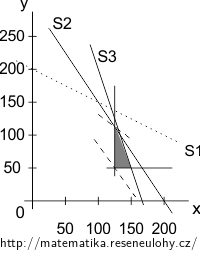
Stejnou metodou vyřešte pozměněný příklad, kde cílem neni maximalizace zisku, ale minimalizace nákladů. Přitom jsou známy náklady na výrobu jednoho kubíku směsi B1 (35 ER) a směsi B2 (25 ER).
Varianta 3
K předchozí variantě doplňte ještě požadavek na minimální objem výroby směsi B1 (125 kubíků za den) a směsi B2 (50 kubíků za den).
Varianta 4
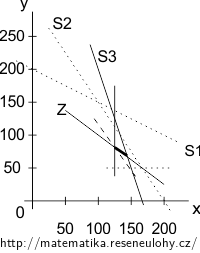
Nyní minimalizujte náklady jako v třetí varaintě za předpokladu, že denní zisk bude přesně 70.000 ER.
Varianta 5
Cílem je opět maximalizace zisku (jako v první variantě), přitom ale dodržte podmínky na minimální objem výroby (třetí varianta).
Varianta 6
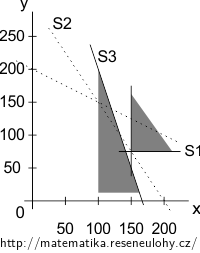
Opět maximalizujte zisk, ale minimální velikost objemu má být 150 kubíků směsi B1 a 75 kubíků směsi B2.
Varianta 7
Převeďte poslední variantu na úlohu LP ve tvaru s minimalizací a rovností.