Image of a cube
Task number: 4423
A linear map \(f:\mathbb R^3\to\mathbb R^3\) transforms a cube \(ABCDEFGH\) into a parallelepiped so that \(f(A)=\mathbf 0\), \(f(B)=(4,-3{,}2)^T\), \(f(D)=(-8{,}3,7)^T\) and \(f(E)=(5,-2,-2)^T\).
Determine images of the remaining four vertices of the cube.
Solution
For simplicity, assume that it is a unit cube with vertex \(A\) at the origin and its vertices \(B, D\) and \(E\) form the standard basis.
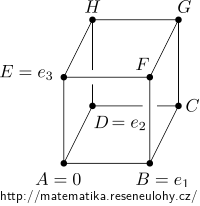
We involve the linearity of \(f\), namely:
\(f(C)=f(B+D)=f(B)+f(D)=(4,-3{,}2)^T+(-8{,}3,7)^T=(-4{,}0,9)^T\), \(f(F)=f(B+E)=f(B)+f(E)=(4,-3{,}2)^T+(5,-2,-2)^T=(9,-5{,}0)^T\), \(f(G)=f(B+D+E)=f(B)+f(D)+f(E)=(4,-3{,}2)^T+(-8{,}3,7)^T+(5,-2,-2)^T=(1,-2{,}7)^T\), \(f(H)=f(D+E)=f(D)+f(E)=(-8{,}3,7)^T+(5,-2,-2)^T=(-3{,}1,5)^T\).In fact, any cube with \(A\) at the origin suffices, since we have not used the specific coordinates of the points \(B, D\) and \(E\) in any way. For \(A\ne\mathbf 0\), the map \(f\) would not be linear. In this case, it would be an affine bijection because the images of the three linearly independent vectors would be linearly independent, but the origin preimage would not be the origin.
Answer
Images of the remaining four vertices are \(f(C)=(-4{,}0,9)^T\), \(f(F)=(9,-5{,}0)^T\), \(f(G)=(1,-2{,}7)^T\) and \(f(H)=(-3{,}1,5)^T\).Comment
However, if the images of the vertices \(B,D\) and \(E\) were linearly dependent, the zero vector need no longer be a preimage of the zero vector, i.e. \(A=\boldsymbol 0\)
But in these cases we get the same solution. Since it is a cube, the differences \(B-A\) and \(C-D\) yield the same vector. Hence \(f(B-A)=f(C-D) \Rightarrow f(B)-f(A)=f(C)-f(D) \Rightarrow f(C)=f(B)+f(D)-f(A)=f(B)+f(D)\).
Similarly for the other vertices.



