Platonic solids
Task number: 2690
Determine the angle between the main diagonal of a cube and some of its sides. Also determine the angle between a side of a regular tetrahedron and an edge to the remaining vertex. Determine the angle between the diagonal of the regular octahedron and some of its sides.
How are these angles related?
What is the volume of the unit tetrahedron and of the unit octahedron (i.e. with unit side lengths)?
Resolution
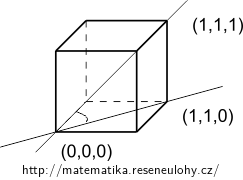
Cube: the angle between the diagonal \(\mathbf x^T=(1, 1, 1)\), and its projection into the bottom side \(\mathbf y^T=(1, 1, 0)\) is \(\cos\alpha_1=\frac{\sqrt{6}}{3}\), \(\alpha_1\doteq 35^\circ\).
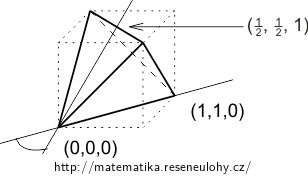
Tetrahedron: If we choose its vertices as \((0, 0, 0)\), \((0, 1, 1)\), \((1, 0, 1)\) and \(\mathbf x^T=(1, 1, 0)\), we get the projection \(\mathbf y^T=(\frac{1}{2}, \frac{1}{2}, 1)\), \(\cos\alpha_2=\frac{\sqrt{3}}{3}\), \(\alpha_2\doteq 55^\circ\).
(Note that the angle is the same regardles whether the tertahedron has side length 1 or \(\sqrt 2\).)
By use of \(\cos{\alpha}=\sin(\frac{\pi}2-\alpha)\) we get that \(\alpha_1+\alpha_2=\frac{\pi}2\).
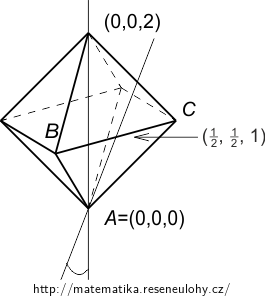
Octahedron: We place vertices at \(A=(0, 0, 0)\), \(B=(1, 0, 1)\), \(C=(0, 1, 1)\), \((-1, 0, 1)\), \((0, -1, 1)\) a \(\mathbf x^T=(0, 0, 2)\). Then the projection of \(\mathbf x\) to the triangle \(ABC\) is a multiple of the vector \(\mathbf y^T=(\frac{1}{2}, \frac{1}{2}, 1)\). Hence \(\cos\alpha_3=\frac{\sqrt{6}}{3}\), \(\alpha_3\doteq 35^\circ\) – the same angle we have calculated on the cube.
The height of the unit tetrahedron is the sine of the calculated angle, i.e. \(\frac{\sqrt{6}}{3}\). The base has height \(\frac{\sqrt{3}}{2}\), hence \(V=\frac{\sqrt{2}}{12}\)
The unit octahedron is composed from two pyramids with the unit square triangle as the basis and whose height \(d\) is half of the octahedron's diagonal. \(V=\frac{2}{3}d\). As \(d\) is half of the diagonal in the square we get \(V=\frac{\sqrt{2}}{3}\).



