Kubické grafy Vizingovy třídy II
Úloha číslo: 3283
Nalezněte nekonečnou množinu hranově 3-souvislých kubických grafů, které jsou Vizingovy třídy II, neboli jejichž chromatický index je 4.
Nápověda
Hledejte operaci, která nedovolí obarvit hrany kubického grafu třemi barvami, ale zvýší počet vrcholů.
Řešení
Nahradíme vrchol stupně tři třemi navzájem spojenými vrcholy, přičemž každý bude incidentní s jednou hranou vedoucí do původního vrcholu. Nový graf má stejný chromatický index jako původní graf, protože tři zmíněné hrany musejí mít různé barvy v každém hranovém 3-obarvení, existuje-li.
Pokud je graf Vizingovy třídy I, pak existuje rozklad hran na 3 perfektní párování, že každá doplněk každého je disjunktní sjednocení kuržnic. Pokud doplněk každého párování obsahuje lichou kružnici, ukázali jsme, že graf je Vizingovy třídy II.
Nyní stačí najít libovolný kubický graf Vizingovy třídy II, například Petersenův graf \(P\). \(P\) má 15 hran. Nejmenší kružnice má délku 5. Vezměme nějaké párování. Pokud jeho doplňkem jsou dvě kružnice, musí mít obě délku 5 a tudíž jsou liché. Pokud by byla jen jedna, je to Hamiltonovská kružnice a tu Petersenův graf nemá. Tedy \(P\) je Vizingovy třídy II.
Nahrazováním vrcholů trojúhelníky můžeme z Petersenova grafu vytvořit libovolně velký graf Vizingovy třídy II.
Varianta
Zkonstruujte libovolně velké grafy požadovaných vlastností a navíc bez trojúhelníků.
Řešení
Mějme nějaký dostatečně velký 3-souvislý kubický graf bez trojúhelníků, může být i hranově 3-obarvitelný. V něm zvolíme libovolný vrchol \(v\). Přidáme kopii \(P\) a v něm zvolíme libovolně vrchol \(w\). Tyto dva grafy sloučíme do jednoho tak, že vrcholy \(v\) a \(w\) odstraníme a hrany, které vedly do \(v\) napojíme na hrany, které vedly do \(w\). Vznikne tak graf \(G\), o kterém chceme, ukázat, že je Vizingovy třídy II.
Uvažme libovolné 3-obarvení výsledeného grafu. Nově napojené hrany budou buď všechny v různých barevných třídách (perfektních párováních) nebo ve stejné, protože zbytek \(P\) má lichý počet vrcholů.
První případ odpovídá situaci, kdy do \(w\) vedou hrany tří barev v 3-obarvení \(P\), což je nemožné.
Ve druhém případě si stačí všimnout, že doplněk zmíněného perfektního párování obsahuje na \(P\) kružnici délky 9. Jde o dva izomorfní případy, viz obrázek.
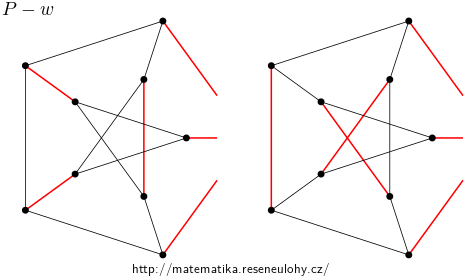
Všimněte si, že začneme-li s grafem bez čtyřúhelníků, neobjeví se ve výsledku ani ty.




