Zobrazení na nekonečných množinách
Úloha číslo: 3360
Najděte zobrazení následujících vlastností:
Varianta
Bijekci mezi \(\mathbb N\) a \(\mathbb Z\).
Nápověda
Zkuste prvky \(\mathbb N\) zobrazovat ’na střídačku’.
Řešení
Jedním z možných řešení je zobrazení je \(f(2k+1)=k\) pro \(k\in\{0{,}1, \dots \}\) a \(f(2k)=-k\) pro \(k\in\{1{,}2, \dots \}\).
Zobrazení \(f\) je prosté (první předpis dává nezáporné hodnoty a druhý záporné), každý z předpisů je prostá lineární funkce.
Zobrazení je na, protože nezáporná \(k\) jsou vzorem \(2k+1\), zatímco záporná \(k\) jsou vzorem \(-2k\).Varianta
Bijekci mezi \(\mathbb N\) a \(\mathbb N^2\).
Nápověda
Jinými slovy, váš úkol je postupně projít všechny prvky \(\mathbb N^2\) (žádný nevynechat, každý projít přesně jednou).
Řešení
Jednou z možností je upořádat body nekonečné mřížky \(\mathbb N^2\) do posloupnosti a bijekce je dána pořadím prvku v této posloupnosti. Jedna z možných posloupností je znázorněna na obrázku.
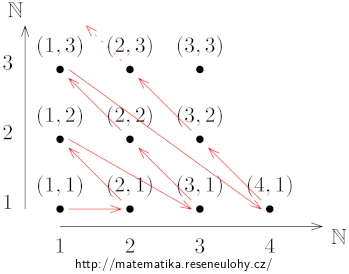
Toto uspořádání lze popsat zobrazením \(f:\mathbb N^2 \to \mathbb N\) pomocí předpisu \(f((u,v))=v+\sum\limits_{i=1}^{u+v-1} i\). Zobrazení \(f\) je prosté a na, a proto je bijekcí. Jeho inverze \(f^{-1}\) je bijekcí z \(\mathbb N\) do \( \mathbb N^2\).
Řešení
Jiný postup je založen na pozorování, že každé přirozené číslo \(n\) lze jednoznačně zapsat jako součin lichého čísla a mocniny dvou (včetně případu \(2^0\)), neboli \(n=2^{u-1}(2v-1)\), kde \(u\) a \(v\) jsou přirozená čísla. Potom zobrazení dané předpisem \(g(n)=(u,v)\) je bijekce mezi \(\mathbb N\) a \(\mathbb N^2\).
Varianta
Prosté zobrazení z \(\mathbb Q^+\) do \(\mathbb N\). (Nebo dokonce zkonstruujte bijekci.)
Nápověda
Zkuste nějak využít předchozí varianty.
Řešení
Každé kladné racionální číslo reprezentujeme zlomkem \(\frac{p}q\), kde \(p\) a \(q\) jsou nesoudělná přirozená čísla. Tento zlomek odpovídá dvojici \((p,q)\).
Označme symbolem \(h\) zobrazení, které kladnému racionálnímu číslu \(\frac{p}q\) přiřadí dvojici \((p,q)\). Jde o prosté zobrazení z \(\mathbb Q^+\) do \(\mathbb N^2\), protože různá racionální čísla odpovídají různým zlomkům. Zobrazení \(h\) není na, protože soudělná dvojice nejsou v oboru hodnot \(h\).
Pokud složíme zobrazení \(h\) se zobrazením \(f\) z předchozí varianty, potom získáme prosté zobrazení \(\mathbb Q^+ \to \mathbb N\).
Bijekci je možné například získat tak, že při konstrukci uspořádání podle obrázku vynecháme všechny soudělné dvojice (spojnice takového bodu s počátkem obsahuje jiný mřížový bod). Toto zobrazení ošem nemá jednoduchý popis. Jinou metodou je využití řetězových zlomků nebo nekonstruktivní důkaz pomocí Cantorovy–Bernsteinovy věty.



