Antiřetězce a řetězce z Hasseova diagramu
Úloha číslo: 3408
Varianta
Řešení
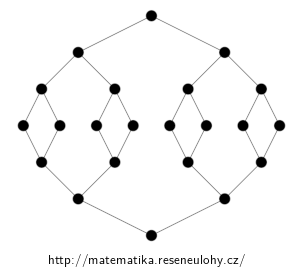
Každý nejdelší řetězec má sedm prvků. Jeden z možných nejdelších řetězců je vyznačen modře.
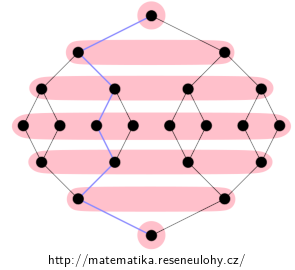
Uspořádání lze pokrýt sedmi antiřetězci, vyznačenými červeně. V uspořádání nemůže být delší řetězec, protože by podle Dirichletova principu obsahoval alespoň dva prvky z nějakého antiřetězce a ty by musely být porovnatelné i neporovnatelné zároveň. Uvědomte si ale, že existují i jiná pokrytí sedmi antiřetězci a že ani není nutné, aby antiřetězce byly disjunktní.
Největší antiřetězec je osmiprvkový, je pro toto částečné uspořádání jednoznačný a je vyznačený červeně v následujícím obrázku.
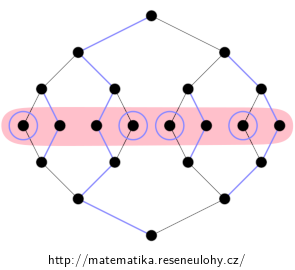
Maximalita délky řetězce se dokáže obdobně. Uspořádání lze pokrýt celkem osmi řetězci, vyznačených modře, z nichž čtyři jednoprvkové jsou zakroužkovány. Proto nemůže obsahovat antiřetězec o devíti prvcích, neboť dva prvky antiřetězce by ležely ve stejném řetězci a to není možné.
Varianta
Řešení
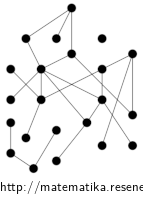
Nejdelší řetězec délky 6 a pokrytí šesti antiřetězci je např:
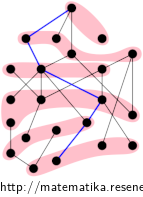
Nejdelší antiřetězec délky 10 a pokrytí desíti řetězci je např: