Změna souvislosti při odebrání vrcholu
Úloha číslo: 4551
Varianta (jednoduchá L1)
\(G\) je nesouvislý a obsahuje vrchol \(u\), že \(G\setminus u\) je hranově dvousouvislý.Řešení
Stačí vzít cyklus \(C_3\) a k němu přudat \(u\) jako izolovaný vrchol.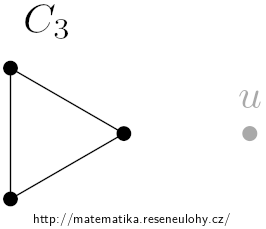
Varianta (jednoduchá L1)
\(G\) je hranově dvousouvislý a obsahuje \(u\), že \(G\setminus u\) je nesouvislý.Řešení
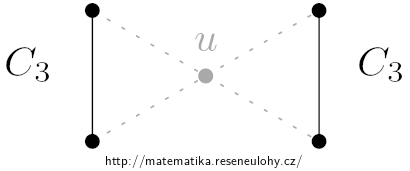
Lze vzít např. dva cykly \(C_3\), z každého zvolit jeden vrchol a tyto spojit do vrcholu \(u\).
Sjednocení dvou hranově \(k\)-souvislých grafů je opět \(k\)-souvislý graf.
Varianta (jednoduchá L1)
\(G\) je nesouvislý a obsahuje \(u\), že \(G\setminus u\) je hranově \(k\)-souvislý.Řešení
Podobně jako v první variantě lze přidat izolovaný vrchol \(u\) k úplnému grafu \(K_{k+1}\).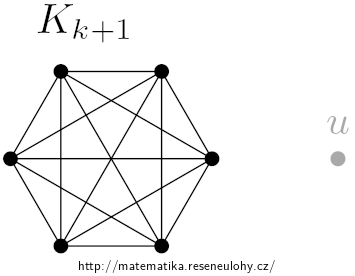
Varianta (jednoduchá L1)
\(G\) je hranově \(k\)-souvislý a obsahuje \(u\), že \(G\setminus u\) je nesouvislý.Řešení
Podobně jako ve druhé variantě lze vzít dva \(K_{k+1}\), z každého zvolit jeden vrchol a tyto spojit do vrcholu \(u\).
Varianta (středně těžká L2)
Pro daná \(k\) a \(l\) sestrojte \(G\), že odebráním vhodného vrcholu se hranová souvislost změní z \(k\) na \(l\), formálně: \(\forall k,l\ \exists G, u: k_e(G)=k \land k_e(G\setminus u)=l\).Řešení
Pokud \(l>k\) pak stačí ke \(K_{l+1}\) přidat nový vrchol \(u\) stupně \(k\).
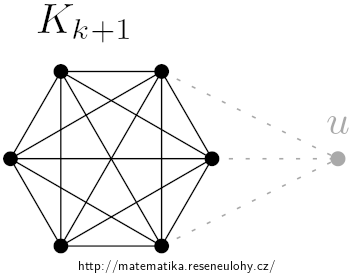
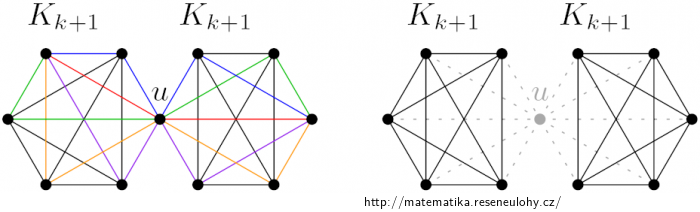
Pro \( l<k \) je možné vzít dva \(K_{k+1}\) spojené přes \(u\) a do tohoto grafu přidat dalších \(l\) nových hran. (Ty musejí vést z jednoho \(K_{k+1}\setminus u\) do druhého.)
Stačí si všimnout, že těchto \(l\) hran je třeba pro nalezení \(l\) hranově disjunktních cest mezi dvěma vrcholy, kde jeden je v první \(K_{k+1}\setminus u\) a druhý v druhé. (Uvnitř \(K_{k+1}\setminus u\) je dokonce \(k-1\) hranově disjunktních cest mezi libovolnými dvěma vrcholy.)
Varianta (těžká L3)
Pro dané \(k\) sestrojte \(G\), že pro každé \(l<k\) lze odebráním vhodného vrcholu snížit hranovou souvislost z \(k\) na \(l\), formálně: \(\forall k\ \exists G\ \forall l < k\ \exists u: k_e(G)=k \land k_e(G\setminus u)=l\).Řešení
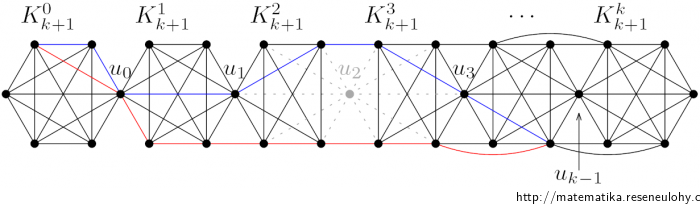
Podobně jako v předchozí variantě, jen konstrukci několikrát zopakujeme. Vezmeme \(k+1\) kopií \(K_{k+1}\), označené \(K_{k+1}^0,\dots,K_{k+1}^k\). V každé kopii \(K_{k+1}^i\) zvolíme dva různé vrcholy \(v_i,w_i\).
Tyto kopie spojíme do řetězce sloučením vrcholů \(w_i,v_{i+1}\) do vrcholu \(u_i\) pro všechna \(i\in\{0,\dots,k-1\}\). Navíc mezi \(K_{k+1}^i\) a \(K_{k+1}^{i+1}\) přidáme \(i\) nových hran.
Ze stejného důvodu jako v předchozí variantě platí, že odebráním \(u_l\) klesne hranová souvislost na \(l\).
Varianta (jednoduchá L1)
Pro daná \(k\) a \(l\) sestrojte \(G\), že odebráním vhodného vrcholu se vrcholová souvislost zvýší z \(k\) na \(l\), formálně: \(\forall k < l\ \exists G, u: k_v(G)=k \land k_v(G\setminus u)=l\).Řešení
Použijeme stejný graf jako dříve: ke \(K_{l+1}\) přidáme nový vrchol \(u\) stupně \(k\).
