Turnajové zápasy
Úloha číslo: 4516
Varianta
Každý tým hrál přesně s pěti týmy ve své kategorii?Řešení
Pro kategorii \(A\) takový plán možný není, protože by z každého z 21 vrcholů vycházelo 5 hran. Každá hrana má dva konce, tedy by \(\frac{21{\cdot} 5}2\) odpovídalo počtu hran, což ale není celé číslo.
Pro kategorii \(B\) je možné navrhnout plán turnaje, možností je mnoho. Např. je možné vzít disjunktní sjednocení dvou \(K_6\) nebo graf dvacetistěnu, nebo vrcholy očíslovat \(\{0,\dots,11\}\) a každé \(i\) spojit s \(i-2,i-1,i+1,i+2 \) a \(i+6 \pmod{12}\), viz obrázek.
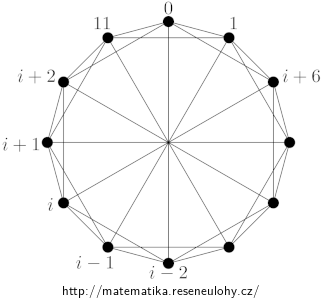
Varianta
Každý tým v kategorii \(A\) hrál přesně se čtyřmi týmy v kategorii \(B\) a všechny týmy v kategorii \(B\) hrály se stejným počtem týmů v kategorii \(A\) (t.j. existuje nějaké číslo \(b\) takové, že každý tým v kategorii \(B\) hraje s \(b\) týmy)?Řešení
V tomto případě by plán turnaje by odpovídal bipartitnímu grafu, kde týmy kategorie \(A\) by tvořily jednu stranu a týmy kategorie \(B\) druhou.
V každého vcholu množiny \(A\) vychází 4 hrany, tedy z množiny \(A\) vychází celkem 84 hran. To musí odpovídat \(b\cdot 12\) hranám vedoucím do \(B\), a odtud \(b=7\).
I takový graf je možné sestavit, např. jako disjunktní sjednocení tří \(K_{7{,}4}\).



