Cubic graphs of Vizing class II
Task number: 4099
Find an infinite set of edge 3-connected cubic graphs, which are Vizing class II, i.e. whose chromatic index is 4.
Hint
Look for an operation that does not allow you to color the edges of a cubic graph with three colors, but increases the number of vertices.
Solution
We replace the vertex of degree three with three paurwise adjacent vertices, each incident with one edge leading to the original vertex. The new graph has the same chromatic index as the original graph, because the three edges mentioned must have different colors in each edge 3-coloring, if any.
If the graph is of Vizing class I, then there is a decomposition of the edges into 3 perfect matchings such that the complement of each is a disjoint union of cycles. If the complement of any perfect matching contains an odd cycle, the graph is of Vizing class II.
Now all we have to do is find any cubic graph of Vizing class II, for example the Petersen graph \( P \). \( P \) has 15 edges. The smallest cycle has a length 5. Consider any matching. If it is complemented by two cycles, they must both have length 5 and are therefore odd. If there was only one, it would be a Hamiltonian circle, but the Petersen graph is not Hamiltonian. Thus \( P \) is Vizing class II.
By replacing the vertices with triangles, we can create an arbitrarily large graph of Vizing class II from the Petersen graph.
Variant
Construct graphs of the required properties of any size and, in addition, without triangles.
Solution
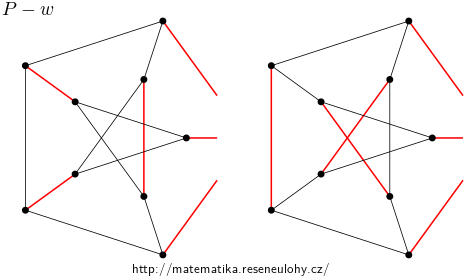
Let’s have a sufficiently large 3-connected cubic graph without triangles, it can also be 3-colorable. In it, we choose any vertex \( v \). Add a copy of \( P \) and arbitrarily select a vertex \( w \). We combine these two graphs into one so that we remove vertices \( v \) and \( w \) and connect the edges that led to \( v \) to the edges that led to \( w \). This yields a graph \( G \), which we want to show to be of Vizing class II.
Consider any 3-coloring of the resulting graph. The newly connected edges will be either all in different color classes (perfect matchings) or in the same, because the rest of \( P \) has an odd number of vertices.
The first case corresponds to a situation, where the edges of three colors in a 3-coloring \( P \) lead to \( w \), which is impossible.
In the second case, it is enough to note that the complement of the mentioned perfect pairing contains on the \( P \) a cycle of length 9. These are two isomorphic cases, see the picture.
Note that if we start with a graph without quadrilaterals, neither will appear in the result.




