Úplné grafy na toru
Úloha číslo: 3273
Které úplné grafy \(K_n\) lze vnořit, t.j. nakreslit bez křížení hran, na torus?
Nápověda
Využijte Eulerovou formuli pro torus.
Alternativně lze vyjít z Heawoodovy formule.
Řešení
Řešení přes Eulerovu formuli:
Pro \(K_n\) platí: \(|V|(|V|-1) = 2|E|\) a \(|F| \leq \frac{2}{3}|E|\). Eulerova formula pro plochy vyššího rodu zní: \(|V| + |F| = |E| + 2 - g\). Torus má \(g = 2\). Dosazením získáváme: \[ \begin{eqnarray*} |V| + |F| &=& |E| + 2 - g \\ |V| + \frac{2}{3} |E|&\geq& |E| \\ 6|V| + 4|E| &\geq& 6|E| \\ 6|V| - 2|E| &\geq& 0\\ 6n -n^2 + n &\geq& 0 \\ n^2 -7n &\leq& 0 \\ (n-7) &\leq& 0 \\ \end{eqnarray*} \]
Řešení přes Heawoodovu formuli:
Projektivní rovina má Eulerovu charakteristiku \(\chi = 0\) a Heawoodova mez vychází \(h(\chi) = \lfloor (7 + \sqrt{49-24{\cdot} 0})/2 \rfloor= 7\)
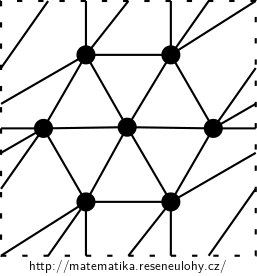
V obou případech vyšla horní mez 7, tedy grafy větší než \(K_7\) nelze vnořit. Nakreslit \(K_7\) lze například tak, že nejprve se nakreslí cyklus \(C_6\), tak abychom dovnitř mohli přidat univerzální vrchol, jako na obrázku.
Odpověď
Největší úplný graf, který lze nakreslit na torus, je \( K_7 \).




