Complete graph on the torus
Task number: 4055
Which complete graphs \( K_n \) can be embedded, i.e. drawn without crossing edges, into the torus?
Hint
Use Euler’s formula for the torus.
Alternatively, use Heawood’s formula.
Solution
Solution via Euler’s formula:
For \( K_n \): \( | V | (| V | -1) = 2 | E | \) and \( | F | \leq \frac {2} {3} | E | \). Euler’s formula for surfaces of higher genus is: \( | V | + | F | = | E | + 2 - g \). The torus has \( g = 0 \). By substituting we get: \[ \begin {eqnarray*} |V| + |F| &=& |E| + 2 - g \\ |V| + \frac{2}{3} |E|&\geq& |E| \\ 6|V| + 4|E| &\geq& 6|E| \\ 6|V| - 2|E| &\geq& 0\\ 6n -n^2 + n &\geq& 0 \\ n^2 -7n &\leq& 0 \\ (n-7) &\leq& 0 \\ \end {eqnarray*} \]
Solution via Heawood’s formula:
The torus has Euler characteristic \( \chi = 0 \) and the Heawood bound yields \( h (\chi) = \lfloor (7 + \sqrt {49-24{\cdot} 0}) / 2 \rfloor = 7 \)
In both cases, the upper bound is 7, i.e. graphs larger than \( K_7 \) cannot be embedded. You can draw \( K_7 \), for example, starting by the cycle \( C_6 \) so that we can add a universal vertex inside, as in the picture..
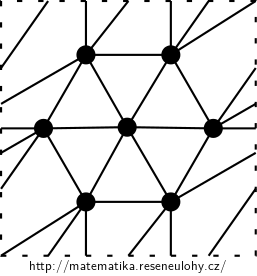
Answer
The largest complete graph that can be drawn on the torus is \( K_7 \).




