Extrémy
Úloha číslo: 3034
Nalezněte globální a lokální extrémy funkcí, a načrtněte jejich grafy.
Varianta 1
\(\displaystyle f(x)=\frac{|2x-1|}{(x-1)^2} \)
Řešení
Definiční obor funkce je \(\mathbb R\setminus \{1\}\). Funkce je na obou intervalech \((-\infty,1)\) a \((1,\infty)\) spojitá.
Nejprve vyšetříme limity v krajních bodech definičního oboru.
\(\displaystyle \lim_{x\to -\infty} \frac{|2x-1|}{(x-1)^2}= \lim_{x\to -\infty} \frac{1-2x}{x^2-2x+1}= \lim_{x\to -\infty} \frac{\frac{1}{x^2}-\frac{2}{x}}{1-\frac2x+\frac1{x^2}}=0 \)
\(\displaystyle \lim_{x\to \infty} \frac{|2x-1|}{(x-1)^2}= \lim_{x\to \infty} \frac{2x-1}{x^2-2x+1}= \lim_{x\to \infty} \frac{\frac{2}{x}-\frac{1}{x^2}}{1-\frac2x+\frac1{x^2}}=0 \)
\(\displaystyle \lim_{x\to 1} \frac{|2x-1|}{(x-1)^2}= \lim_{x\to 1} \frac{2x-1}{(x-1)^2}= \infty \)
Pro \(x< \frac 12\) je derivace funkce \(f\)
\(f'= \left(\frac{1-2x}{(x-1)^2} \right)'= \frac{-2(x-1)^2-(1-2x)\cdot 2(x-1)} {(x-1)^4}= \frac{2x}{(x-1)^3} \)
a pro \(x> \frac 12\) dostaneme
\(f'= \left(\frac{2x-1}{(x-1)^2} \right)'= \frac{2(x-1)^2-(2x-1)\cdot 2(x-1)} {(x-1)^4}= \frac{-2x}{(x-1)^3} \)
V bodě \(x=\frac 12\) je derivace funkce \(f\) nespojitá, protože
\(\displaystyle \lim_{x\to \frac12^-} f'(x)= \lim_{x\to \frac12^-} \frac{2x}{(x-1)^3}= -8 \)
zatímco
\(\displaystyle \lim_{x\to \frac12^+} f'(x)= \lim_{x\to \frac12^+} \frac{-2x}{(x-1)^3}= 8 \)
Nulový bod derivace: \(f'=0\) pro \(x=0\).
Dále pro \(x\in (-\infty, 0)\) je \(f'(x)>0\), tedy \(f\) je rostoucí.
Pro \(x\in \left(0,\frac12\right)\) je \(f'(x)<0\), tedy \(f\) je klesající a v \(x=0\) je lokální maximum.
Pro \(x\in \left(\frac 12{,}1\right)\) je \(f'(x)>0\), tedy \(f\) je rostoucí a v \(x=\frac12\) je lokální minimum.
Pro \(x\in (1,\infty)\) je \(f'(x)<0\), tedy \(f\) je klesající.Lokální minimum v bodě \(\left(\frac12{,}0\right)\) je zároveň globálním minimem.
Výsledek
Funkce je shora neomezená, nemá tedy globální maximum. Lokální maximum je v bodě \((0{,}1)\), globální minimum je v bodě \(\left(\frac12{,}0\right)\).

Varianta 2
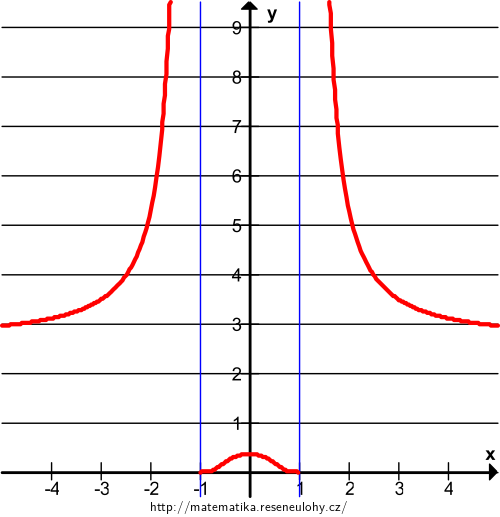
\(\displaystyle f(x)=\exp\left(\frac{x^2+1}{x^2-1}\right) \)
Řešení
Definiční obor funkce je \(\mathbb R\setminus \{-1{,}1\}\). Funkce je sudá, stačí vyšetřit její chování na \(\langle 0,\infty)\) Funkce je na obou intervalech \(\langle0{,}1)\) a \((1,\infty)\) spojitá.
Limity v krajních bodech \(D_f\):
\(\displaystyle \lim_{x\to \infty} \exp\left(\frac{x^2+1}{x^2-1}\right)=e^1=e \)
\(\displaystyle \lim_{x\to 1^-} \exp\left(\frac{x^2+1}{x^2-1}\right)=0 \)
\(\displaystyle \lim_{x\to 1^+} \exp\left(\frac{x^2+1}{x^2-1}\right)=\infty \)
Derivace funkce \(f\) – s úpravou výrazu \(\frac{x^2+1}{x^2-1}=1+\frac2{x^2-1}\)
\(\displaystyle f'=\exp\left(\frac{x^2+1}{x^2-1}\right)\frac{-4x}{(x^2-1)^2} \)
Nulový bod derivace: \(f'=0\) pro \(x=0\).
Pro \(x\in (0{,}1)\cup (1,\infty)\) je \(f'(x)<0\), tedy \(f\) je klesající a v \(x=0\) je lokální maximum.
Výsledek
Funkce je shora neomezená, nemá tedy globální maximum. Lokální maximum je v bodě \((0,e)\). Obor hodnot je \((0,\infty)\), globální minimum se nenabývá.
{
Varianta 3
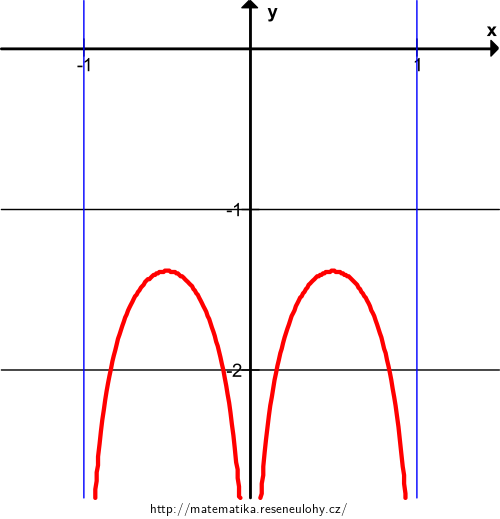
\(\displaystyle f(x)=\ln\left(|x|-x^2\right) \)
Řešení
Jde o sudou funkci, stačí ji vyšetřit na \(\langle0,\infty)\). Definiční obor funkce \(f\): Logaritmus je definován pro kladné hodnoty argumentu, tedy \(|x|-x^2>0\). Odtud \(D_f= (-1{,}0)\cup(0{,}1)\). Na obou intervalech je funkce spojitá.
Limity v krajních bodech \(D_f\):
\(\displaystyle \lim_{x\to 0^+}\ln\left(|x|-x^2\right)= \lim_{x\to 0^+}\ln\left((1-x)x\right)= \ln(1)\cdot \lim_{x\to 0^+}\ln x=-\infty \)
\(\displaystyle \lim_{x\to 1^-}\ln\left(|x|-x^2\right)= \lim_{x\to 1^-}\ln\left(x(1-x)\right)= \ln(1)\cdot \lim_{x\to 1^-}\ln(1-x)=-\infty \)
Derivace funkce \(f\) – pro \(x>0\):
\(f'= \left(\ln\left(x-x^2\right)\right)'= \frac{1-2x}{x-x^2} \)
Nulový bod derivace: \(f'(x)=0\) pro \(x=\frac12\)
Pro \(x\in \left(0,\frac12\right)\) je \(f'(x)>0\), tedy \(f\) je rostoucí.
Pro \(x\in \left(\frac 12{,}1\right)\) je \(f'(x)<0\), tedy \(f\) je klesající a v \(x=\frac12\) je lokální maximum, které je zároveň globálním maximem.Výsledek
Funkce je zdola neomezená, nemá tedy globální minimum. Globální maxima jsou v bodech \(\left(-\frac12,\ln\frac14\right)\) a \(\left(\frac12,\ln\frac14\right)\).
Varianta 4
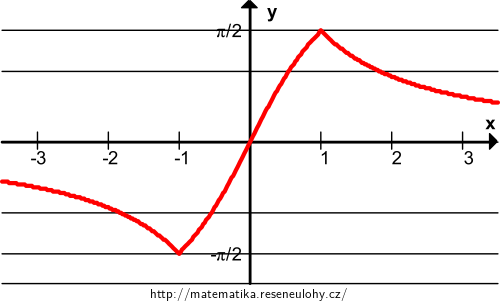
\(\displaystyle f(x)=\arcsin\left(\frac{2x}{1+x^2}\right) \)
Řešení
Jde o lichou funkci, stačí ji vyšetřit na \(\langle0,\infty)\). Definiční obor funkce \(f\): Arkussinus je definován na intervalu \(\langle-1{,}1\rangle\), tedy pro kladná \(x\) požadujeme, aby platilo: \(\frac{2x}{1+x^2}\le 1 \iff 2x \le 1+x^2 \iff 0\le (1-x)^2\), což je vždy splněno. Odtud \(D_f=\mathbb R\). Funkce \(f\) je navíc spojitá.
Limity v krajních bodech \(D_f\):
\(\displaystyle \lim_{x\to \infty} \arcsin\left(\frac{2x}{1+x^2}\right)= \lim_{t\to 0} \arcsin t = 0 \)
Derivace funkce \(f\):
\(\displaystyle f'= \frac1{\sqrt{1- \left(\frac{2x}{1+x^2}\right)^2 }}\cdot \frac{2(1+x^2)-4x^2}{\left(1+x^2\right)^2}= \frac{2(1-x^2)}{\sqrt{\left(1-x^2\right)^2}}\cdot\frac{1}{1+x^2}= \frac{2(1-x^2)}{\sqrt{\left(1-x^2\right)^2}}\cdot\frac{1}{1+x^2} \)
Tento výraz není definován pro \(x=1\). Ověříme, jestli \(f'(1)\) lze určit limitou. Máme \( \lim_{x\to 1^-}f'(x)=1 \) zatímco \( \lim_{x\to 1^+}f'(x)=-1 \), funkce tedy nemá pro \(x=1\) derivaci. \(D_{f'}=\mathbb R\setminus\{-1{,}1\}\).
Derivace \(f'\) nemá žádné nulové body.
Pro \(x\in (0{,}1)\) je \(f'(x)>0\), tedy \(f\) je rostoucí.
Pro \(x\in (1,\infty)\) je \(f'(x)<0\), tedy \(f\) je klesající a v \(x=1\) je lokální maximum, které je zároveň globálním maximem.Výsledek
Globální maximum je v bodě \(\left(1,\frac\pi2\right)\) a globální minimum v bodě \(\left(-1,-\frac\pi2\right)\).