Extrema
Task number: 3047
Find the global and local extrema of the functions, and sketch their graphs.
Variant 1
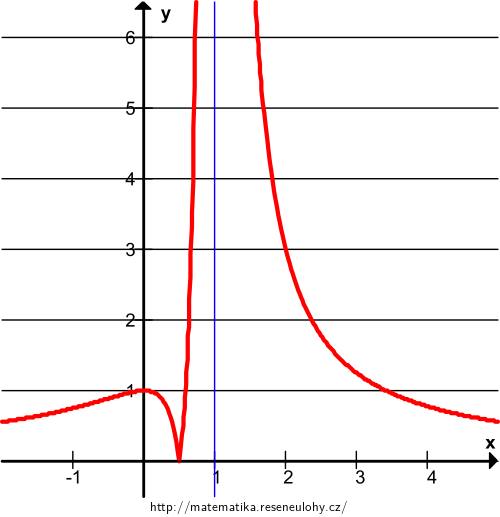
\(\displaystyle f(x)=\frac{|2x-1|}{(x-1)^2} \)
Resolution
The domain of definition of the function is \(\mathbb R\setminus \{1\}\). The function is continuous on the intervals \((-\infty,1)\) and \((1,\infty)\).
First we investigate the limits at the boundary points of the domain of definition.
\(\displaystyle \lim_{x\to -\infty} \frac{|2x-1|}{(x-1)^2}= \lim_{x\to -\infty} \frac{1-2x}{x^2-2x+1}= \lim_{x\to -\infty} \frac{\frac{1}{x^2}-\frac{2}{x}}{1-\frac2x+\frac1{x^2}}=0 \)
\(\displaystyle \lim_{x\to \infty} \frac{|2x-1|}{(x-1)^2}= \lim_{x\to \infty} \frac{2x-1}{x^2-2x+1}= \lim_{x\to \infty} \frac{\frac{2}{x}-\frac{1}{x^2}}{1-\frac2x+\frac1{x^2}}=0 \)
\(\displaystyle \lim_{x\to 1} \frac{|2x-1|}{(x-1)^2}= \lim_{x\to 1} \frac{2x-1}{(x-1)^2}= \infty \)
For \(x< \frac 12\) the derivative of the function \(f\) is
\(f'= \left(\frac{1-2x}{(x-1)^2} \right)'= \frac{-2(x-1)^2-(1-2x)\cdot 2(x-1)} {(x-1)^4}= \frac{2x}{(x-1)^3} \)
and for \(x> \frac 12\) we obtain
\(f'= \left(\frac{2x-1}{(x-1)^2} \right)'= \frac{2(x-1)^2-(2x-1)\cdot 2(x-1)} {(x-1)^4}= \frac{-2x}{(x-1)^3} \)
At the point \(x=\frac 12\) the derivative of the function \(f\) is discontinuous, because
\(\displaystyle \lim_{x\to \frac12^-} f'(x)= \lim_{x\to \frac12^-} \frac{2x}{(x-1)^3}= -8 \)
while
\(\displaystyle \lim_{x\to \frac12^+} f'(x)= \lim_{x\to \frac12^+} \frac{-2x}{(x-1)^3}= 8 \)
Critical point: \(f'=0\) for \(x=0\).
For \(x\in (-\infty, 0)\) we have \(f'(x)>0\), so \(f\) is increasing.
For \(x\in \left(0,\frac12\right)\) we have \(f'(x)<0\), so \(f\) is decreasing and \(x=0\) is a local maximum.
For \(x\in \left(\frac 12{,}1\right)\) we have \(f'(x)>0\), so \(f\) is increasing and \(x=\frac12\) is a local minimum.
For \(x\in (1,\infty)\) we have \(f'(x)<0\), so \(f\) is decreasing.The local minimum at the point \(\left(\frac12{,}0\right)\) is also a global minimum.
Result
The function is unbounded above, so it does not have a global maximum. There is a local maximum at the point \((0{,}1)\) and a global minimum at \(\left(\frac12{,}0\right)\).
Variant 2
\(\displaystyle f(x)=\exp\left(\frac{x^2+1}{x^2-1}\right) \)
Resolution
The domain of definition of the function is \(\mathbb R\setminus \{-1{,}1\}\). The function is even, so we need only investigate its behavior on the interval \(\langle 0,\infty)\) The function is continuous on the intervals \(\langle0{,}1)\) and \((1,\infty)\).
Limits at boundary points of the domain of definition \(D_f\):
\(\displaystyle \lim_{x\to \infty} \exp\left(\frac{x^2+1}{x^2-1}\right)=e^1=e \)
\(\displaystyle \lim_{x\to 1^-} \exp\left(\frac{x^2+1}{x^2-1}\right)=0 \)
\(\displaystyle \lim_{x\to 1^+} \exp\left(\frac{x^2+1}{x^2-1}\right)=\infty \)
The derivative of the function \(f\) – transforming the expression \(\frac{x^2+1}{x^2-1}=1+\frac2{x^2-1}\)
\(\displaystyle f'=\exp\left(\frac{x^2+1}{x^2-1}\right)\frac{-4x}{(x^2-1)^2} \)
Critical point: \(f'=0\) for \(x=0\).
For \(x\in (0{,}1)\cup (1,\infty)\) we have \(f'(x)<0\), so \(f\) is decreasing and \(x=0\) is a local maximum.
Result
The function is unbounded above, so it does not have a global maximum. There is a local maximum at the point \((0,e)\). The range of the function \((0,\infty)\), and it does not reach a global minimum.

Variant 3
\(\displaystyle f(x)=\ln\left(|x|-x^2\right) \)
Resolution
This is an even function, so we need only investigate it on the interval \(\langle0,\infty)\). The domain of definition of \(f\): The logarithm is defined for positive values of its argument, so \(|x|-x^2>0\). Hence \(D_f= (-1{,}0)\cup(0{,}1)\). The function is continuous on both intervals.
Limits at boundary points of \(D_f\):
\(\displaystyle \lim_{x\to 0^+}\ln\left(|x|-x^2\right)= \lim_{x\to 0^+}\ln\left((1-x)x\right)= \ln(1)\cdot \lim_{x\to 0^+}\ln x=-\infty \)
\(\displaystyle \lim_{x\to 1^-}\ln\left(|x|-x^2\right)= \lim_{x\to 1^-}\ln\left(x(1-x)\right)= \ln(1)\cdot \lim_{x\to 1^-}\ln(1-x)=-\infty \)
The derivative of the function \(f\) – for \(x>0\):
\(f'= \left(\ln\left(x-x^2\right)\right)'= \frac{1-2x}{x-x^2} \)
Critical point: \(f'(x)=0\) for \(x=\frac12\)
For \(x\in \left(0,\frac12\right)\) we have \(f'(x)>0\), so \(f\) is increasing.
For \(x\in \left(\frac 12{,}1\right)\) we have \(f'(x)<0\), so \(f\) is decreasing and \(x=\frac12\) is a local maximum, which is also a global maximum.Result
The function is unbounded below, so it has no global minimum. There are global maxima at the points \(\left(-\frac12,\ln\frac14\right)\) and \(\left(\frac12,\ln\frac14\right)\).

Variant 4
\(\displaystyle f(x)=\arcsin\left(\frac{2x}{1+x^2}\right) \)
Resolution
This is an odd function, so it suffices to investigate it on the interval \(\langle0,\infty)\). The domain of definition of \(f\): The arcsin function is defined on the interval \(\langle-1{,}1\rangle\), so for positive \(x\) we require that: \(\frac{2x}{1+x^2}\le 1 \iff 2x \le 1+x^2 \iff 0\le (1-x)^2\), which is always satisfied. Hence \(D_f=\mathbb R\). The function \(f\) is continuous everywhere.
Limits at boundary points of \(D_f\):
\(\displaystyle \lim_{x\to \infty} \arcsin\left(\frac{2x}{1+x^2}\right)= \lim_{t\to 0} \arcsin t = 0 \)
Derivative of the function \(f\):
\(\displaystyle f'= \frac1{\sqrt{1- \left(\frac{2x}{1+x^2}\right)^2 }}\cdot \frac{2(1+x^2)-4x^2}{\left(1+x^2\right)^2}= \frac{2(1-x^2)}{\sqrt{\left(1-x^2\right)^2}}\cdot\frac{1}{1+x^2}= \frac{2(1-x^2)}{\sqrt{\left(1-x^2\right)^2}}\cdot\frac{1}{1+x^2} \)
This expression is undefined for \(x=1\). We check whether we can determine \(f'(1)\) using limits. We have \( \lim_{x\to 1^-}f'(x)=1 \) while \( \lim_{x\to 1^+}f'(x)=-1 \), so the function has no derivative at \(x=1\). \(D_{f'}=\mathbb R\setminus\{-1{,}1\}\).
The derivative \(f'\) is not zero at any point.
For \(x\in (0{,}1)\) we have \(f'(x)>0\), so \(f\) is increasing.
For \(x\in (1,\infty)\) we have \(f'(x)<0\), so \(f\) is decreasing and \(x=1\) is a local maximum, which is also a global maximum.Result
There is a global maximum at the point \(\left(1,\frac\pi2\right)\) and a global minimum at the point \(\left(-1,-\frac\pi2\right)\).




