Collection of Maths Problems

The number of order relations

Task number: 4148

• Hint

  Proceed systematically according to the number of comparable pairs.

• Solution

  Linear Arrangement – \( 4! = 24 \) options.

  One incomparable pair:
  between maximum elements – 12 options
  between " middle " elements – 12 options
  between minimal elements – 12 options

  Two incomparable pairs:
  two maximum and two minimum elements – 6 options
  two maximum elements and one smallest – 24 options
  two minimal elements and one largest – 24 options

  Three incomparable elements:
  with the largest element – 4 options
  with the smallest element – 4 options
  without the largest and smallest element – \( 4! = 24 \) options.

  Discontinuous partial arrangements

  2 components with two elements – 12 options

  2 components, one with one, the other with three elements:
  with a linear arrangement on three elements – \( 4! = 24 \) options.
  with the largest element on the three elements – 12 options
  with the smallest element on the three elements – 12 options

  3 components – 12 options

  4 components – 1 option

  The Hasse diagrams for the partial orders are:

  

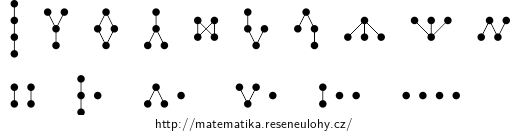
• Answer

  There are 219 partial orders on the four elements, 16 of which are non-isomorphic.