Two unmatchable edges
Task number: 4045
Construct a cubic graph without bridges that contains two non-adjacent edges that do not together belong to any common matching.
Hint
Explore matching of a small complete graph and also possible operations with this graph.
Solution
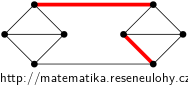
The complete graph \(K_4\) has a unique partition into perfect matchings. Take two copes of \(K_4\), in each choose an edge, delete these two and then add edges between vertices of degree two to make this graph connected.
The newly added edges can be extended to a unique matching, so it is easy to pick one of them and a non-matchable edge from the rest, see the picture.