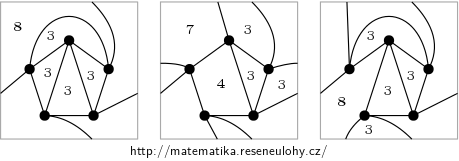
Different drawings of K5 on torus
Task number: 4058
Find (at least) two different drawings of the complete graph \( K_5 \) on the torus.
We consider different to be those in which it is not possible to convert one to the other by a continuous mapping of the whole torus, i.e. by deformations and symmetries.
Can you find different drawings of \( K_5 \) that have the same numbers of faces of the same size?
Hint
It is necessary to find two drawings whose multi-sets of face sizes differ. This ensures that the drawings are different.
Indeed, drawings that have faces of the same sizes can be different, because it also depends on the mutual position of the faces.
Solution
Examples of different drawings are shown in the figure. The face sizes (measured by the length of the circumferential walk) are marked in the figure
Even the first and last drawings are different. The first has one vertex incident to all triangles, while the third does not.