Quadrangular faces
Task number: 4098
Find a graph that can be drawn on a torus so that all faces are bounded by a four-cycle and have the chromatic number three.
Hint
The graph can have an odd cycle as a subgraph, but not necessarily as a face.
Solution
For example, the toroidal grid \( 3 \times 3 \) contains a triangle, and it can be colored with three colors, see the picture.
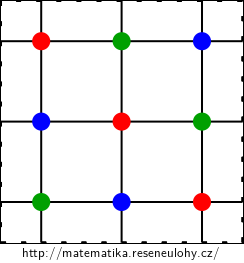
Variant
Try to find a graph with the same drawing conditions, but to have the chromatic number four.
Hint
Try to start with the grid again, but this time wind it on the torus in a skewed way.
Algebraic tools, namely Cayley graphs , can be used to describe such a graph. Cayley graph for the group \( G \) and the set of generators \( X \subseteq G \) is a graph on \( | G | \) vertices \( V \), where each vertex corresponds to one element of the group \( G \) and the edges correspond to the composition with generators.
In other words, there is a bijection \( f: V \rightarrow G \) such that the vertices of \( u, v \) are joined by an edge, iff there is \( x \in X \) that \( f (u) x = f (v) \) or \( f (u) x^{-1} = f (v) \). The Cayley graph is usually denoted as \( Cay (G, X) \).
Examples: \( C_5 = Cay (\mathbb Z_5, \{1 \}) \), \( K_5 = Cay (\mathbb Z_5, \{1{,}2 \}) \).
Solution
Take the Cayley graph \( G = Cay (\mathbb Z_{13}, \{1{,}5 \}) \). This graph can be drawn on a torus with quadrangular faces.
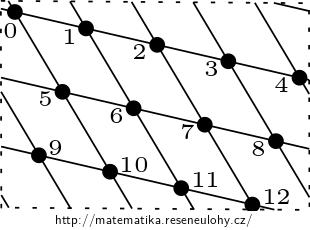
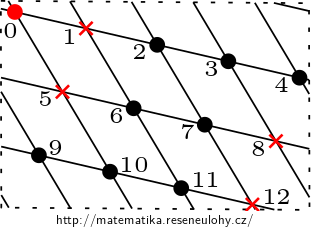
It contains an odd cycle of 0-12, so its chromatic number is at least 3.
We show by a contradiction that the chromatic number is at least 4. If \( G \) could be colored with three colors, one of the colors would have to be used at least five times. Without loss of generality, let it be red and let 0 be red. Red cannot be used on its neighbors, so four of the remaining eight vertices must be red. On these vertices we can find an eight-cycle 2-3-4-9-10-11-6-7, so either red are 2,4,10 and 6; or 3,9,11 and 7. The first option is excluded due to the edge \( (2{,}10) \) the second due to \( (3{,}11) \).
However, coloring with four colors exists, indeed one of the colors needs to be used only once.
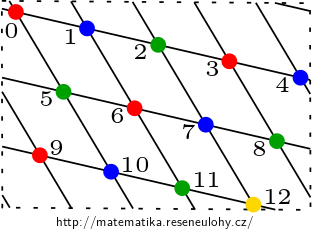
Variant
Can you find a graph that has a chromatic number four and whose drawing in the projective plane would have all the faces quadrangular?
Solution
Just cleverly draw the graph \( K_4 \). It has three faces, they are marked in color in the picture.





