Rectangle tiling
Task number: 3878
How many ways can you tile a rectangle \( n \times k \) by using tiles \( 1 \times 2 \)?
Variant
Solve for \(k=2\).
Hint
Denote the number of tilings by \(a_n\), then find a recurrence for \(a_n\) and resolve it with help of a generating function. Set the initial values for \( a_0 \), etc. accordingly.
Solution
The tiling of the rectangle \(n\times 2 \) can be obtained either from a tiling of a rectangle of length \( n-1 \) with the last tile being vertical, or from a tiling of a rectangle of length \( n-2 \) with the last two tiles laid horizontally.
We get \(a_n=a_{n-1}+a_{n-2}\), while \(a_1=1\) and \(a_2=2\).
Answer
The number of tilings of an \(n\times 2\) rectangle is the \(n\)-th Fibonnaci number \(\frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}2\right)^n-\left(\frac{1-\sqrt{5}}2\right)^n\right)\).
Variant
And how many different ways of tiling by the same tiles has the rectangle when \(k=3\)?
Solution
As in the previous case, we try to convert the tiling of the rectangle to the case with smaller \(n\). The first observation is that \(n\) is even.
The rectangle \( 2 \times 3 \) can be tiled in three ways. For \(k\ge 2\), the rectangle \( 2k \times 3 \) can be tiled in two ways so that it cannot be decomposed into two smaller tiled rectangles of height 3, see the figure.
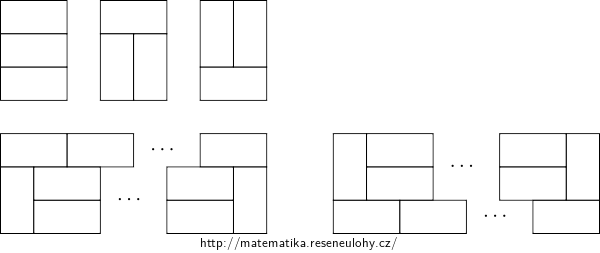
We get the following recurrence:
\(b_n=3b_{n-2}+2b_{n-4}+2b_{n-6}+…+2b_{0}\), přičemž dodefinujeme \(b_0=1\).
If we subtract the next equation from the previous one:
\(b_{n-2}=3b_{n-4}+2b_{n-6}+…+2b_{0}\),
we get \(b_n-4b_{n-2}+b_{n-4}=0\), which can already be solved like other recurrences.
This charakteristic polynomial has roots \(2\pm\sqrt3\).
From \(b_0=1\) and \(b_2=3\) we get a linear combination of powers of roots with coefficients \(\frac12\pm\frac{\sqrt3}6\).
Answer
The number of tilings of the rectangle \( n \times 3 \) for an even \( n \) is equal to \(\left(\frac12+\frac{\sqrt3}6\right)\left(2+\sqrt3\right)^{\frac{n}2}+ \left(\frac12-\frac{\sqrt3}6\right)\left(2-\sqrt3\right)^{\frac{n}2}\).
For odd \( n \) such a rectangle cannot be tiled.





