Triangle and 4-cycle
Task number: 4017
The edges of the complete \( K_n \) graph are colored red and blue. Prove that in this graph we find either a blue triangle or a red 4-cycle for:
Variant
\(n=9\).
Solution
Choose any vertex \( u \). Either it is incident with at least four blue edges or at least five red.
In the first case, if these blue edges are not to be added to the blue triangle, we must always add a red edge, thus creating a red \( K_4 \), which contains \( C_4 \).
In the other case, we must not create a red path of length two between the vertices adjacent to \( u \) over the red edges. The red edges therefore form a matching on these five vertices, which is a graph with at least three components. If we select one vertex from each component, we get a blue triangle.
Variant
\(n=8\).
Solution
We proceed similarly to the previous variant. If none of the situations described in the previous variant should occur, it means that three blue edges lead to \( u \), whose opposite ends \( M = \{m_1, m_2, m_3 \} \) induce a red triangle, and four other red edges whose opposite ends \( C = \{c_1,…, c_4 \} \) induce a blue 4-cycle with red diagonals.
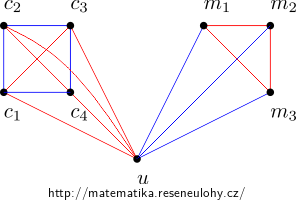
If a red edge from \( c_1 \) goes to the set \( M \), all edges between \( c_3 \) and \( M \) would have to be blue so as not to get red \(C_4 \) (two cases: either passing \( c_1, u, c_3 \) and the common ‘red’ neighbor \( c_1 \) and \( c_3 \) or passing \( c_1, c_3 \) and their two neighbors in \( M \)).
Similarly, from either \( c_2 \) or \( c_4 \), only blue edges lead to \( M \). However, in this way we get a blue triangle from two vertices from \( C \) and one from \( M \).



