Collection of Maths Problems

Complete graphs in the projective plane

Task number: 4054

• Hint

  Use Euler’s formula for the projective plane.

  Alternatively, use Heawood’s formula.

• Solution

  Solution via Euler’s formula:

  For \( K_n \): \( | V | (| V | -1) = 2 | E | \) and \( | F | \leq \frac {2} {3} | E | \). Euler’s formula for surfaces of higher genus is: \( | V | + | F | = | E | + 2 - g \). The projective plane has \( g = 1 \). By substituting we get: \[ \begin {eqnarray*} | V | + | F | & = & | E | + 2 - g \\ | V | + \frac {2} {3} | E | & \geq & | E | + 1 \\ 6 | V | + 4 | E | & \geq & 6 | E | + 6 \\ 6 | V | - 2 | E | & \geq & 6 \\ 6n -n ^ 2 + n & \geq & 6 \\ n ^ 2 -7n + 6 & \leq & 0 \\ (n-6) (n-1) & \leq & 0 \\ n & \leq & 6 \\ \end {eqnarray*} \]

  Solution via Heawood’s formula:

  The projective plane has Euler characteristic \( \chi = 1 \) and the Heawood bound yields \( h (\chi) = \lfloor (7 + \sqrt {49-24}) / 2 \rfloor = 6 \)

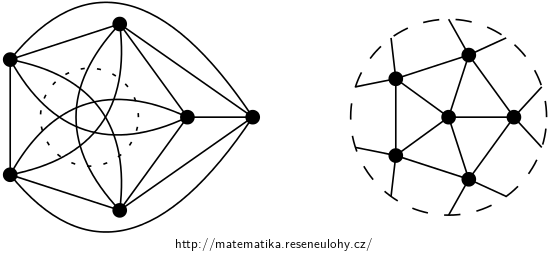
  In both cases, the upper bound is 6, i.e. graphs larger than \( K_6 \) cannot be embedded. You can draw \( K_6 \), for example, starting by the complete graph \( K_5 \) so that it has a cross-cap inside and the outer face has length 5, as in the picture on the left. To the right is the drawing after the circular inversion of the cros-scap.

  

• Answer

  The largest complete graph that can be drawn in the projective plane is \( K_6 \).