Complements of planar graphs
Task number: 4248
Show that the complement of a planar graph with 11 vertices cannot be planar, and find an example of the largest possible planar graph whose complement is planar.
Solution
There are 55 edges on 11 vertices, so either \( G \) or \( \overline G \) would have to have at least 28 edges.
However, planar graphs on 11 vertices have at most \( 3 {\cdot}11-6 \) edges, so a graph with 28 edges on 11 vertices cannot be planar.
An example of a planar graph on eight vertices, the complement of which is planar, is shown in the figure (the positions of the vertices are unchanged).
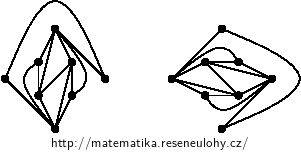
Note that the complement is even isomorphic to the original.
Note: There are no planar graphs on the nine vertices that have a planar complement. See the article by Battle, Harary, Kodama from 1962: http://www.ams.org/journals/bull/1962-68-06/S0002-9904-1962-10850-7/S0002-9904-1962-10850-7.pdf



