Exact number of automorphisms
Task number: 3599
For each natural number \(n\) construct a graph \(G_n\) that has exactly \(n\) automorphisms, i.e. isomorphisms \(G_n\to G_n\).
Solution
\(K_1\) has one automorphism, \(K_2\) has two.
The cycle \(C_k\) has \(2k\) automorphisms \(f\)– we have \(k\) choices for \(f(v_1)\) and then we can assign \(f(v_2)\) to one of the two neighbors of \(f(v_1)\). Then the remaining vertices are uniquely determined. This construction solves the problem for all even \(n=2k\).
We can construct graphs for odd \(n\) using a similar principle, but we must replace the edges of \(C_n\) with more complicated graphs so that \(f(v_2)\) will be uniquely determined by the choice of \(f(v_1)\). We can achieve this e.g. by replacing each edge with a path of length three, where we add 1 leaf to the first interior vertex and two leaves to the second such vertex; see the picture below.
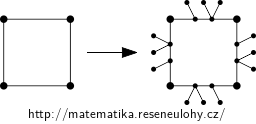
If the original cycle has vertices \(v_1,…,v_k\) in clockwise order, then in the transformed graph every automorphism maps the vertex \(v_1\) to some vertex of degree two. Then the image of \(v_2\) is uniquely determined: it is the first vertex of degree two that follows \(f(v_1)\) in a clockwise direction.
There exist other similar constructions.



