Petersen graph is not planar
Task number: 4243
Prove in two ways that the Petersen graph is not planar.
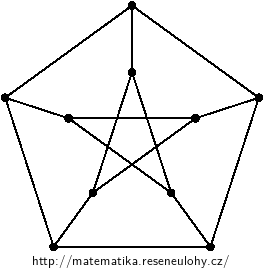
Solution
The first way: by using the Kuratowski’s theorem, because it contains a subdivision of \( K_ {3{,}3} \)
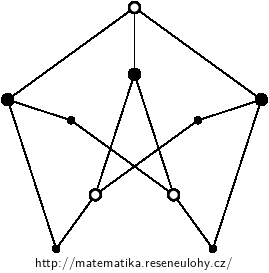
The second way: the contractions maintain planarity, but by the contraction of the matching between the outer and inner five-cycle we get a non-planar graph \( K_5 \).
Third way: Petersen’s graph has no triangles or fourcycles. If it was planar, it should, as a consequence of Euler’s formula, satisfy the estimate \( | E_P | \le \frac53 (| V_P | -2) \), which it does not satisfy.




