Plane coloring
Task number: 4019
Show that if the points of the Euclidean plane are arbitrarily colored with three colors, then two points of the same color can always be found at the unit distance.
Solution
You need to find a suitable graph at the points of distance 1, which has the chromatic number 4.
Such graphs exist, one is depicted in the following picture:
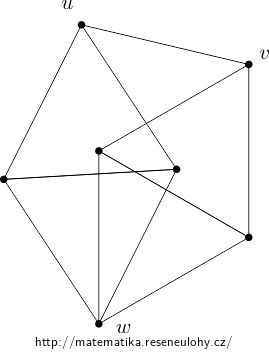
If we color the graph with three colors, due to the triangles the vertices \( u \) and \( w \) as well as \( v \) and \( w \) would have the same color, which is impossible.




