Isomorphism between two concrete graphs
Task number: 3592
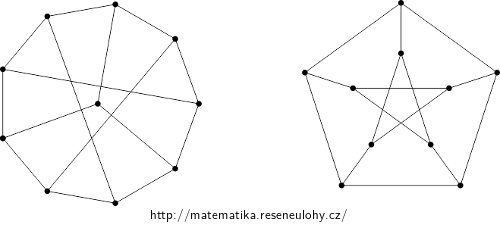
Find an isomorphism of the graphs in the picture:
Next, decide which of them is isomorphic to the third graph \( F \), given by the formula: \( V_F=\binom{\{1,…,5\}}2\), \(E_F=\{(A,B): A\cap B=\emptyset\}\).
Hint
First, test the necessary conditions for the existence of an isomorphism. Then try to construct the isomorphism by analyzing the cases.
Draw the graph \( F \).
Solution
All three graphs have the same number of vertices – 10, same number of edges – 15, even vertices of the same degree – in all, all vertices have a degree of 3.
However, the necessary but not sufficient conditions are met.
Isomorphism of general graphs is generally a difficult task and no efficient algorithm is known for it. In this task we can try to find him by ‘brute force‘, i.e. by analyzing cases.
We will simply try to display vertex # 1 in \( G \) and its three neighbors on any vertex in \( H \) and its three neighbors. (In our case, any choice will work, in general, you should try all the options for choosing these four images in \( H \).)
Note that vertices 1, 2, 5, 8, and 4 form a cycle in \( G \), so we find in \( H \) a cycle of length five that contains images 1, 2, and 4, and we place images of vertices 5 and 8 on it. In our case, there are two such possibilities and both lead to the result. This may not be the case in general, and if one option fails, others should be tried.
The rest is already given unambiguously, because the as yet unoccupied neighbor of Figure 2 must be Figure 6. Similarly for 4 and 9; 5 and 7; 8 and 10.
It remains to mechanically verify whether the found image retains the edges. We have already used 10 edges in the construction, it is enough to verify that the remaining five are preserved: \( (5{,}7), (7{,}9), (9{,}6), (6{,}10), (10 , 5) \).
The fact that the edges are preserved follows from the fact that the display is simple and both graphs have the same number of edges.
For the graph \( F \) we proceed similarly, only it is advisable to draw the graph first.
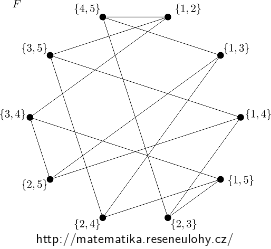
The isomorphism between \( F \) and \( H \) is obtained, for example, by the composition of isomorphisms between \( F \) and \( G \) and between \( G \) and \( H \). We can also realize that the relation ‘to be isomorphic‘ is equivalence (not only on graphs).
Answer
Yes, all three graphs are isomorphic to each other, it is a so-called Petersen graph.
For example, the following isomorphism can be found between \( G \) and \( H \):
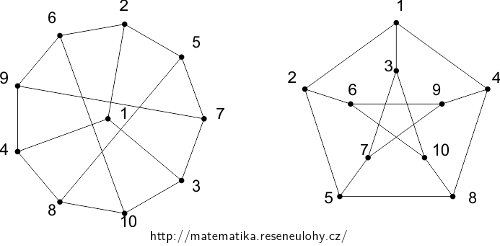
One of the possible isomorphisms \( f: G \to F \) can be described, for example, by the table:
\( \begin{array}{c|cccccccccc} u &1&2&3&4&5&6&7&8&9&10 \\ f(u) & \{1{,}2\} & \{3{,}4\} & \{3{,}5\} & \{4{,}5\} & \{1{,}5\} & \{2{,}5\} & \{2{,}4\} & \{2{,}3\} & \{1{,}3\} & \{1{,}4\} \end{array} \)



