Collection of Maths Problems

Chromatic index of complete graph

Task number: 4066

• Hint

  Distinguish the cases of even and odd \( n \).

• Solution

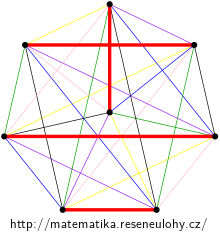
  For even \( n \), draw the vertices of the graph into the vertices of a regular \( (n-1) \) -gon and place the last vertex in its center. Any edge leading from center to the boundary can be extended to a perfect matching so that the added edges are perpendicular to the starting edge.

  These matchings are disjoint to each other and prove that \( \chi’(K_n) = \Delta (K_n) = n-1 \), see figure.

  

  For odd \( n \) we notice that in each maximum matching, one vertex remains uncovered. Therefore, each maximum matching has \( \frac{n-1}{2} \) edges. The graph \( K_n \) has a total of \( \frac{n (n-1)}{2} \) edges, so each edge coloring must have at least \( n \) classes.

  Since \( K_n \) is a subgraph of \( K_{n + 1} \), we get \( \chi'(K_n) \leq \chi' (K_{n + 1}) = n \).

• Answer

  The chromatic index of the complete graph \( K_n \) is \( \chi (K_n) = \begin{cases} n-1 & n \text{ is even} \\ n & n \text{ is odd} \end{cases} \).