Let \(f(x) = x^3 - 12x + 16\).
Domain of definition, range and intersections with axes: The domain of definition of \(f\) is all real numbers, and we will determine the function's range later.
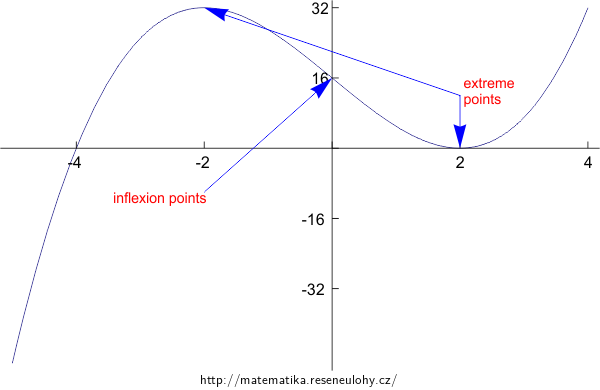
We can factor the function as \(f(x) = (x-2)^2(x+4)\), so it intersects the \(x\)-axis at the points \((-4{,}0)\) and \((2{,}0)\), and intersects the \(y\)-axis at the points \((0, 16)\).
Monotonicity: We have \(f'(x) = 3x^2 - 12 = 3(x-2)(x+2)\). So we have critical points at \(x = \pm 2\). From the factorization we can easily tell that \(f'(x) > 0\) on the intervals \((-\infty, -2)\) and \((2, \infty)\), so the function is increasing on these intervals. Conversely \(f'(x) < 0\) on the interval \((-2, 2)\), where the function is decreasing. So we know that at \(x = -2\) there is a local maximum, namely \(f(-2) = 32\), and at \(x = 2\) there is a local minimum, namely \(f(2) = 0\).
Convexity: Now we compute \(f''(x) = 6x\). So we have \(f''(x) > 0\) for \(x \in (0, \infty)\) and \(f''(x) < 0\) for \(x \in (-\infty, 0)\). So the function is concave on the interval \((-\infty, 0)\) and convex on \((0, \infty)\). At \(x = 0\) we have an inflection point.
Limits at boundary points: We have \(\lim_{x \to \infty} f(x)= \infty\) and \(\lim_{x \to -\infty} f(x)= -\infty\) (as you can surely easily compute). This helps us sketch the graph around "infinities". And now we also know, since \(f\) is continuous, that the range of \(f\) is \(\mathbb R\).
Asymptotes: We have \(\lim_{x \to \infty} f(x)/x = \lim_{x \to -\infty} f(x)/x =\infty\), as you can surely easily compute. From here it follows that the function does not have asymptotes either at \(\infty\) or at \(-\infty\).