Spanning trees
Task number: 2609
Use determinant to calculate the number of spanning trees of the following graphs:
Variant

Solution
The Laplace’s matrix of the graph is
\( L_G=\begin{pmatrix} 4 & -1 & -1 & -1 & -1 \\ -1 & 4 & -1 & -1 & -1 \\ -1 & -1 & 3 & -1 & 0 \\ -1 & -1 & -1 & 3 & 0 \\ -1 & -1 & 0 & 0 & 2 \\ \end{pmatrix} \)
By the theorem on the number of spanning trees
\(\kappa(G)=\det L_G^{11}= \begin{vmatrix} 4 & -1 & -1 & -1 \\ -1 & 3 & -1 & 0 \\ -1 & -1 & 3 & 0 \\ -1 & 0 & 0 & 2 \\ \end{vmatrix} = \begin{vmatrix} 4 & -1 & -1 & -1 \\ -1 & 3 & -1 & 0 \\ -1 & -1 & 3 & 0 \\ 7 & -2 & -2 & 0 \\ \end{vmatrix} = \begin{vmatrix} -1 & 3 & -1 \\ -1 & -1 & 3 \\ 7 & -2 & -2 \\ \end{vmatrix} \)
\( = \begin{vmatrix} -1 & 3 & -1 \\ 0 & -4 & 4 \\ 0 & 19 & -9 \\ \end{vmatrix} =-4 \begin{vmatrix} -1 & 1 \\ 19 & -9 \\ \end{vmatrix} =-4(9-19)=40 \).It is possible to verify the result by a listing of all spanning trees: \(K_4\) has 16 spanning trees and each has two options to join the top vertex (the left or the right edge) – in total 32 possibilities. Otherwise the spanning tree contains both edges incident with the top vertex and then we have 4 options that contain the bottom edge an 4 that do not.
Answer
The graph has 40 spanning trees.
Variant
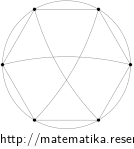
Solution
Laplace’s matrix: \(L_G= \begin{pmatrix} 5 & -2 & 0 & -1 & 0 & -2 \\ -2 & 5 & -2 & 0 & -1 & 0 \\ 0 & -2 & 5 & -2 & 0 & -1 \\ -1 & 0 & -2 & 5 & -2 & 0 \\ 0 & -1 & 0 & -2 & 5 & -2 \\ -2 & 0 & -1 & 0 & -2 & 5\\ \end{pmatrix} \)
Number of spanning trees: \( \kappa(G)=|L_G^{11}|= \begin{vmatrix} 5 & -2 & 0 & -1 & 0 \\ -2 & 5 & -2 & 0 & -1 \\ 0 & -2 & 5 & -2 & 0 \\ -1 & 0 & -2 & 5 & -2 \\ 0 & -1 & 0 & -2 & 5\\ \end{vmatrix} = 960 \)
Answer
The graph has 960 spanning trees.



