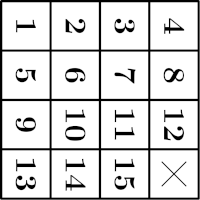
Fifteen
Task number: 2464
Find the criterion for the solvability of the so called “Fifteen”.
This is a puzzle where 15 square stones numbered from 1 to 15 are placed in a \(4\times 4\) grid, but instead of one stone there is a free space that allows to move stones. At the beginning, the stones are arbitrarily shuffled, the aim of the game is to arrange them from 1 to 15.
The goal of this task is to characterize the distributions of stones that can be sorted in this way. To begin, consider the position where the stones are arranged so that the numbers 14 and 15 are interchanged as in the picture.
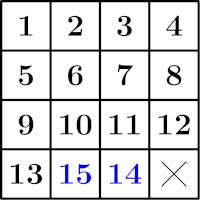
Hint
Consider the following order of the squares:
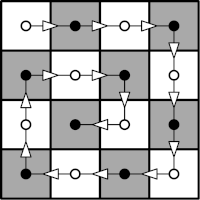
The given position then corresponds to the permutation: \((1{,}2,3{,}4,8{,}12,14{,}15,13{,}9,5{,}6,7{,}11,10)\). Try to derive some rule for such orders.
Resolution
Positions will be represented as numbers of the squares \(1{,}2,…,15\) ordered as they show up on the curve (any other connected curve would be good enough). This is a permutation of \(1,…,15\).
It suffices to argue that any move preserves the sign of the permutation, i.e. solvable ones have positive sign, while non-solvable negative. Any move shifts a stone between positions with odd and even index (on the curve), i.e. the number of stones that have been passed is always even.
Note: Samuel Lloyd (1841–1911), popularized this puzzle in 1878 by declaring that the premium $1.000 will be awarded to anyone, who first finds a sequence of moves that interchanges squares 14 and 15. We see that it is not possible, however, two trick “solutions” are shown in the following pictures.
First trick solution - different placement of empty slot:
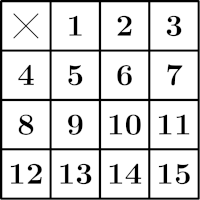
Second trick solution - rotate the grid: