Gershgorin disks
Task number: 4370
Gershgorin's theorem says that every eigenvalue is contained in some Gershgorin disk. But the converse is not true; some disks may not contain any eigenvalue.
It could be proven that if Gershgorin's disks into groups such that each group covers a continuous region of the complex plane, while the regions corresponding to the different groups are disjoint, then each region contains as many eigenvalues as there are disks of which it was formed.
Now use Gershgorin disks to show that in a complex domain the following matrix has at least two distinct eigenvalues, without calculating the eigenvalues:
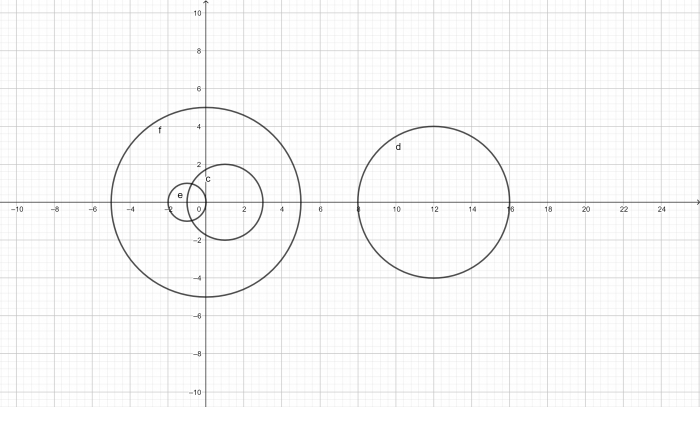
\( \begin{pmatrix} 1&0&-2&0\\ 0&12&0&-4\\ -1&0&-1&0\\ 0&5&0&0 \end{pmatrix}\)Solution
From the matrix, derive four disks in the complex plane with the following centres and radii:
\(\begin{array}{ll} c_1=a_{11}=1,& r_1=|a_{12}|+|a_{13}|+|a_{14}|=2\\ c_2=a_{22}=12,& r_2=|a_{21}|+|a_{23}|+|a_{24}|=4\\ c_3=a_{33}=-1,& r_3=|a_{31}|+|a_{32}|+|a_{34}|=1\\ c_4=a_{44}=0,& r_4=|a_{41}|+|a_{42}|+|a_{43}|=5 \end{array}\)
Since we got two regions, the matrix has at least two different eigenvalues.
In fact, you could calculate that it has four different eigenvalues: \(\lambda_1=10, \lambda_2=2, \lambda_3=\sqrt{3}\) and \(\lambda_4=-\sqrt{3}\).